Introducing the Dot – Dot Simulation

by | Apr 5, 2017

This post describes a new, powerful tool, called a dot-dot simulation, for experiencing function behavior when both the input and output variables of the function describe discrete units.  To use the tool, you enter a function, enter a minimum and maximum value for the domain, as well as a minimum and maximum value for the range.  The tool then allows you to visualize the input and output pairs of the function as side-by-side columns of stacked dots.

Here’s a detailed picture of how the tool works:

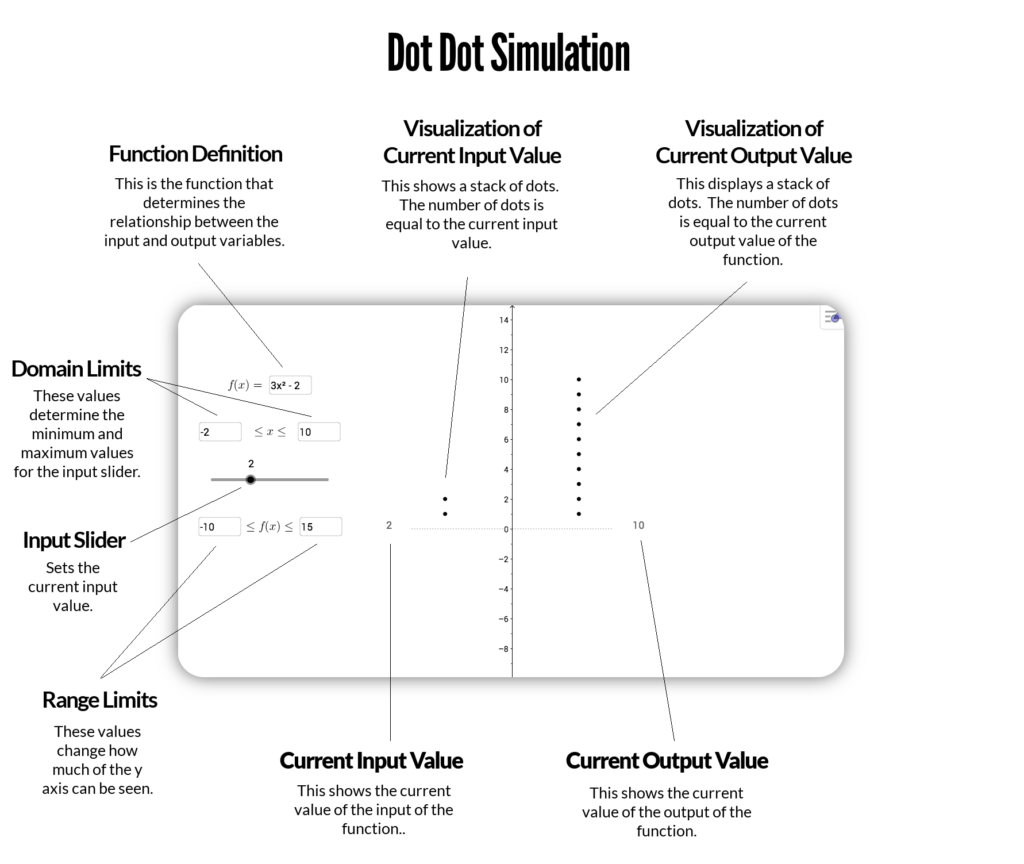
Here’s an image of the tool cycling through some inputs for the function f(x)=0.1x^2:

And here is the tool itself. To acclimate yourself with the tool:

  1. Slide the slider from left to right and notice that it goes from -10 to 10.
  2. Change the minimum and maximum values for x to -6 and 9.  Then slide the slider again and notice that it now goes from -6 to 9.
  3. Notice how the vertical axis goes from -10 to 10.  Change the minimum and maximum values for f(x) to -20 and 30.  Notice how the vertical axis changes to reflect the new range.
  4. Finally, change the function to something other than f(x) = 2x, then slide the slider again and note how the dot stacks reflect the new function’s values.

DOT DOT SIMULATION

 

Finally, here’s a task for you to try that illustrates how easily this tool breathes meaning into even the most obscure functions and situations.

Imagine a story about food pellets and fish.  Let x represent the number of food pellets.  Let f(x) represent the number of fish.  Let f(x)=x^{sin(x)} define the relationship between number of pellets and number of fish.

  1. Create a dot dot simulation for this situation and examine the output for 0 to 100 pellets.
  2. Make up a story that explains this data.

I gave my 7th graders 15 minutes to complete this same task.  Here’s what some of them said.

Student 1:

 

Student 2:

Student 3:

Student 4:

Even though, some of the stories are crude, the exciting thing here is that 7th graders constructed creative, meaningful interpretations of the function f(x)=x^{sin(x)} with confidence.  The dot-dot-simulation was the tool that allowed it.

 

Assembling a New, Scalable Math Education Paradigm

by | Mar 23, 2017

My name is Harry O’Malley.  I am a math teacher.  I am developing techniques, content, and ideas that I believe can be formed together to create a new, scalable math paradigm that is better than the current one.  I have created this blog so that:

  1. I am forced to think through the development of the paradigm more carefully.  I hope that the process of writing about it as it continues to be created will make it better.
  2. I can more easily connect with others about it.  I hope you will react to and use the techniques, content and ideas initiated here and help develop them yourself.

I have been developing these ideas in relative isolation for a number of years, now.  I have been fortunate enough to be able to use them consistently with my students, but I have not formally shared much with you all on the internet.  I only mention this because many of the techniques, content and ideas don’t make perfect sense unless you are aware of how they are organized within and related to the other techniques, content and ideas.  And sharing everything all at once is too daunting.  I will do my best to make things valuable despite the lack of complete context all the time.  I look forward to connecting with you.