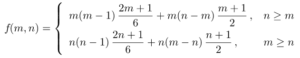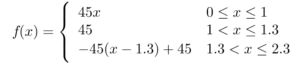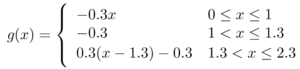Graphs are Overrated. Simulations are the Future.

by | Apr 21, 2017

Graphs of functions seem like they should provide great insight into the behavior of the quantities they describe.  I mean, c’mon.  They’re visual ways to view the relationship.  And that’s how humans experience and understand the world primarily: visually.  Graphs seem perfect, then.  So what’s the problem?

The problem is that graphs don’t look like the quantities they describe.  For example, let’s say the number of birds living in a particular area increased at a relatively constant rate from 10 to 20 over the course of 2 months.  What does this look like?  It looks like a mini-movie that has 10 birds on the screen.  Then, over a period of time, additional birds get added to the movie, one-by-one, until there are twenty.  In other words, it looks something like this:

A graph of this story, on the other hand, looks like this:

For another example, imagine a machine piece that pivots according to the function f(x)=50sin(x) where x is time, in seconds, and f(x) is the pivot angle, in degrees.  Here is what it actually looks like:

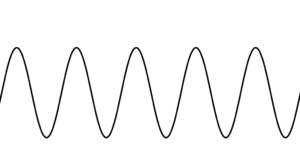
The graph, unfortunately, looks like this:

Humans experience their world as moving, visually changing stories that involve objects engaged in actions:

birds migrating to an area

robot arms swinging back and forth

A graph is a static, visually motionless picture of a single object that bears no resemblance to its source and is not engaged in any action:

slanted line segment

wavy curve

The fact that graphs are currently our go-to way of “visualizing” functions means that our students have almost no chance of understanding what mathematics means.  For a person who isn’t extremely well versed in mapping graphs to direct experience, graphing a function is like translating a paragraph from Spanish to Italian.

Simulations, on the other hand, are like magic.  When designed correctly, they have the ability to translate a symbolic mathematical function into something that even a person with no mathematical knowledge can easily make sense of.  For example, here is the simulation I used to produce the robot arm image above.  The arm is currently set to rotate according to the function f(x)=50sin(x).  Press the play button to see it move.  Then pause the animation and change the function to something else.  Press play again to see how the new function affects the behavior of the arm.  Remember, x is time and f(x) is degrees of rotation.

What about the migrating birds?  Here’s a simulation that allows users to experience changes in the number of discrete objects over time. It’s currently set to simulate our bird example, where the number of birds increases from 10 to 20 over 2 months using the function f(x)=5x+10 over the interval 0 \le x \le 2 where x is time, in months, and f(x) is the number of birds.  Press play to see it in action.  Then pause it, insert any new function you want, and play it again to see how the new function governs the number of objects.  Depending on the function you choose, you may need to adjust the f(x) range so you can see all of the output.

 

 

These simulations allow students to get direct experience with functions that describe concrete contexts.  They can try tons of different functions and immediately see their effect on the quantities they describe.  They can make slight alterations to functions and immediately see how this alteration expresses itself in the actual context.  It’s remarkable.

Using these simulations feels similar to translating a web page.  When you open a web page that is in a different language, it is a wall of meaningless jargon.  Then the button appears at the top asking you if you would like to translate the page.  When you click that translate button and the whole page instantly turns into English, it’s like a floodgate of meaning opens up.

Using these simulations has the same effect.  They take highly abstract symbolic mathematical functions and instantly translate them into direct, meaningful concrete experience.

This creates a completely new type of mathematical literacy.  How fluent are your students in the use of quadratic functions to describe and govern rotations?  How fluent are your students in using trigonometric functions to describe and govern temperature?  How fluent are your students in using inverse functions to describe and govern luminosity?  The answers to these questions will be largely dependent on the number of structured hours your students have spent engaged with simulations like this.

My current goal is to develop a set of standard simulations that can be used to explore the vast majority of contexts and then develop instructional resources to support their use. I genuinely believe that this approach has the ability to drastically affect the future direction of mathematics education.  My upcoming posts will be dedicated to fleshing out this paradigm and releasing new resources related to it.

I hope you have many questions, thoughts, concerns, and additions. Please put them in the comments so we can start a conversation.

Understanding Lillian

by | Apr 17, 2017

Like many of us, I read and watched Fawn Nguyen’s story about Lillian.  I won’t say much here.  Only that it has certainly made me feel and think.  I have three children and I love them deeply.  They are are in pre-school, kindergarten and 2nd grade.  Although Lillian is in 9th grade, I realized that only a short number of years ago, she was the age of my daughter.  This really affected me.  I’m not sure what to do about the whole experience or what it means.  I made a short film to help deepen my relationship with the story and better understand my feelings about it.

 

 

If you haven’t read or seen Fawn’s post, here’s a link:

Lillian

Teaching the Meaning of Mathematics

by | Apr 14, 2017

In 2015, Graham Fletcher posted an article centered around what he calls “Multiplication Subitizing Cards”.  Each card displays a visual representation of a multiplication sentence.  Here’s a picture of one that represents the equation 5 \times 7 = 35:

Here is a link to Graham’s article:

Subitizing to Foster Multiplicative Thinking

And here is a link to the cards themselves:

Multiplication Cards

Graham uses them as a way to develop fluency with mentally figuring out the value of multiplication expressions.  I, in contrast, use them to develop fluency in two areas:

  1. translating visual stimuli into mathematical symbols
  2. translating visual stimuli into verbal mathematical language

Teaching my 4, 6, and 8 year olds to “read” these cards took two lessons:

Lesson 1 consisted of teaching them the meaning of unit rate language, specifically the word per.  I showed them a coin and said “2 sides per coin” and told them “per” just meant “for 1” so the whole thing meant “2 sides for 1 coin”.  Then I showed them a table and said “4 legs per table”.  Then a carton of eggs and said “12 eggs per carton”.  Then I had them take turns finding examples.  My 4 year old pointed to my wife and said “2 eyes per face”.  My 6 year old found a bowl of pinecones, counted them and said “14 pinecones per bowl”.  My 8 year old looked at our kitchen cabinets and said “2 handles per drawer”.  Then we just practiced more.

Lesson 2 happened the next day.  I showed them the multiplication card below and said “How many dots are there in 1 circle”?  They said “2”.  So I said, “So we can say that there are 2 dots per circle” to which they agreed.  Then I showed them a few more cards and asked them to practice using the “per” language:  “4 dots per circle”, “7 dots per circle”, etc.  Finally I introduced them to the sentence “2 dots per circle times 3 circles equals 6 total dots”, carefully pointing to each element in the picture as I said it.  Then I had them repeat that exact language back to me using the same picture.  Then I gave them two more cards that they could easily count, 4 \times 2 = 8 and 3 \times 3 = 9.  Lastly I pulled out the card for 4 \times 7 = 28 as well as the calculator.  As I slowly said the language, “4 dots per circle times 7 circles equals 28”, my finger pressed the corresponding calculator buttons.  After the calculator displayed 28, I carefully counted out all of the dots to show that there were, indeed, a total of 28 dots.  They loved that.  They were amazed. They wanted to try.  So they did.  They practiced until they could take any card and translate it into perfect verbal mathematical language and an accurate sequence of calculator keys.

Here they are in action:

 

This activity illustrates a central math education design principal I am trying to develop and flesh out:

Time spent learning to fluently compute, both mentally and by hand, should be significantly reduced and time spent mapping mathematical language to direct experience should be significantly increased.

Learners should become fluent in the meaning of mathematics.

Experiencing Michael Fenton’s Rectangle World

by | Apr 13, 2017

Today, Michael Fenton wrote a blog that posed the question “How many squares fit inside an m x n rectangle?”  Here is a link to Michael’s article:

How Many Squares?

And here is the solution to his problem:

where m and n are the lengths of the sides of the rectangle and f(m,n) is the number of squares that can fit inside the rectangle.

I found this solution here.

And here is something I designed to help experience the relationships described by this function.  Dragging the black dot allows you to create rectangles with different dimensions.  The number next to the dot expresses the number of squares that can fit inside that rectangle.

Playing with it for just a few minutes reveals tons of interesting and unexpected patterns and ideas for further exploration. What interesting patterns can you find? What new questions do you have after playing with it? I invite you to post them in the comments to further the discussion. Here’s one to get you started. A 4 x 3 rectangle produces 20 squares. A 4 x 21 rectangle produces 200 squares. Hmmm…

Mathematics is a Tool For Storytelling

by | Apr 8, 2017

Mathematics is a tool for storytelling.  To see this, consider my brother.  He is an applied mathematician.  One of his current areas of study is groundwater.  He tries to understand, and help other people understand, what happens to water that is deep within the ground.  He collects data about the water’s behavior at different locations within the ground and then uses mathematics to stitch that data together into a story about what the water is doing.  He’s a story teller.

This says, in a short and succinct way, what I have been trying to express to myself for 10 years but only now fully realized.  I grew up thinking math was about calculating.  In graduate school, I was introduced to the idea that math was all about problem solving.  Now I realize its neither of these things, ultimately.  In the end, mathematics is about story telling.  Let’s explore how with an example.

Here is a video of a hole puncher being squeezed.

It is a simple story that is told using the medium of film.  Translating it into verbal language, we have:

The handle is pressed and the hole punching cylinder moves down. Then pressure on the handle is released and the hole punching cylinder moves back up.

In verbal language, the basic units are words, and those words are formed into stories through the use of sentences.

In mathematical language, the basic units are quantities, and those quantities are formed into stories through the use of functions.

Let’s translate the verbal story into mathematics piece by piece.  “The handle is pressed”, in this case, describes a rotation of the hole puncher’s handle around its pivot point as a function of time.  The two quantities are time, in seconds, and angle of rotation of the hole puncher handle, in degrees.  They are formed into a story by the function:

f(x)=45x

where x is time and f(x) is the angle. By representing the time with a slider and the handle with a line segment, this piece of the story can be visualized using GeoGebra like this:

“…and the hole punching cylinder goes down” describes the vertical position of the cylinder relative to its starting position, in inches, which we’ll call g(x), over time, which is still x.  These quantities are formed into a story by the function:

g(x)=-0.3x

Using a vertical line segment in GeoGebra to represent the hole-punching cylinder, the simulation now looks like this:

And finally, the rest of the story:

…Then pressure on the handle is released and the hole punching cylinder moves back up.

This requires changing the original functions into piecewise ones, describing the handle and cylinder as they travel down, pause briefly, and then travel back up to their starting positions:

Adding this to the simulation completes the story:

This example illustrates the fact that mathematics is a tool for telling stories.  Modern simulation software like GeoGebra allows people to perceive these stories in ways that were impossible a short time ago.  Thinking of mathematics primarily as a story telling tool will drastically reshape the way I instruct and develop learning materials for my students moving forward.