In 2015, Graham Fletcher posted an article centered around what he calls “Multiplication Subitizing Cards”.  Each card displays a visual representation of a multiplication sentence.  Here’s a picture of one that represents the equation :

Here is a link to Graham’s article:

Subitizing to Foster Multiplicative Thinking

And here is a link to the cards themselves:

Multiplication Cards

Graham uses them as a way to develop fluency with mentally figuring out the value of multiplication expressions.  I, in contrast, use them to develop fluency in two areas:

1. translating visual stimuli into mathematical symbols
2. translating visual stimuli into verbal mathematical language

Teaching my 4, 6, and 8 year olds to “read” these cards took two lessons:

Lesson 1 consisted of teaching them the meaning of unit rate language, specifically the word per.  I showed them a coin and said “2 sides per coin” and told them “per” just meant “for 1” so the whole thing meant “2 sides for 1 coin”.  Then I showed them a table and said “4 legs per table”.  Then a carton of eggs and said “12 eggs per carton”.  Then I had them take turns finding examples.  My 4 year old pointed to my wife and said “2 eyes per face”.  My 6 year old found a bowl of pinecones, counted them and said “14 pinecones per bowl”.  My 8 year old looked at our kitchen cabinets and said “2 handles per drawer”.  Then we just practiced more.

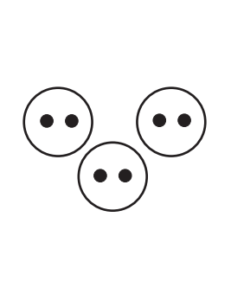
Lesson 2 happened the next day.  I showed them the multiplication card below and said “How many dots are there in 1 circle”?  They said “2”.  So I said, “So we can say that there are 2 dots per circle” to which they agreed.  Then I showed them a few more cards and asked them to practice using the “per” language:  “4 dots per circle”, “7 dots per circle”, etc.  Finally I introduced them to the sentence “2 dots per circle times 3 circles equals 6 total dots”, carefully pointing to each element in the picture as I said it.  Then I had them repeat that exact language back to me using the same picture.  Then I gave them two more cards that they could easily count, and .  Lastly I pulled out the card for as well as the calculator.  As I slowly said the language, “4 dots per circle times 7 circles equals 28”, my finger pressed the corresponding calculator buttons.  After the calculator displayed 28, I carefully counted out all of the dots to show that there were, indeed, a total of 28 dots.  They loved that.  They were amazed. They wanted to try.  So they did.  They practiced until they could take any card and translate it into perfect verbal mathematical language and an accurate sequence of calculator keys.

Here they are in action:

This activity illustrates a central math education design principal I am trying to develop and flesh out:

Time spent learning to fluently compute, both mentally and by hand, should be significantly reduced and time spent mapping mathematical language to direct experience should be significantly increased.

Learners should become fluent in the meaning of mathematics.